数字电路学习笔记（三）：基本逻辑

首次发布于 2019/9/1。原文链接

这几章讲的是逻辑设计的基础：布尔运算。

布尔运算和普通算术运算最大的不同，在于其包括的数集只有 0 与 1（或者“真”和“假”），而算术运算是全数集；所以，布尔运算的学习重点一般在于算式的化简而不是求值。

我们又要回到这幅图了

在开始之前，我们先了解几个概念。

逻辑运算，又叫布尔运算，是通过一系列既定的逻辑规则，对一些逻辑命题进行恒等变形的研究。

基本逻辑，本质上是布尔运算中的运算符，可类比于算术运算中的加减乘除、阶乘乘方等；指示了对逻辑变量的运算规则。有三种简单逻辑、两种特殊逻辑、若干复合逻辑。

真值表，它描述了对于所有可能的自变量取值，因变量的值的情况。它的存在是建立在布尔运算中变量的可能值很少，可以穷举的前提上的。

逻辑图，用示意图的形式表示逻辑运算关系，是抽象化的电路，直观化的算式。

一、非逻辑

众所周知，运算可以分成一元、二元与多元。其中一元运算只有一个：非逻辑 (NOT)。

• 名称：非逻辑
• 算式表示方法： $A'$或$\overline{A}$（本文中采用前者）
• 意义：只有当$A$不发生时，$X$才发生
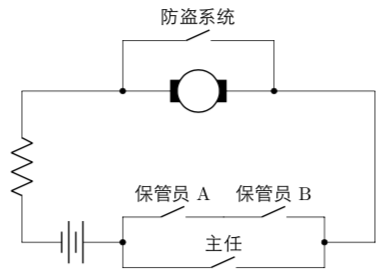
• 等价开关电路：开关与用电器并联（图中防盗系统开关）
• 逻辑符号：

  

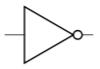
• 真值表：

$A$	$X$
0	1
1	0

观察真值表，可以知道非逻辑本质上是将变量进行了取反。

二、或逻辑

或逻辑 (OR) 是最基础的两个二元逻辑之一。

• 名称：或逻辑
• 算式表示方法：$A+B$
• 意义：只要当$A$或$B$中有一个发生时，$X$就发生
• 等价开关电路：两开关并联（图中保管员开关组与主任开关）
• 逻辑符号：

  

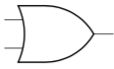
• 真值表：

$A$	$B$	$X$
0	0	0
0	1	1
1	0	1
1	1	1

观察真值表，可以知道或逻辑用加号表示的原因是它类似加法运算，且结果为 1 的概率有 75%（这在某些场合会有用处）。

三、与逻辑

与逻辑 (AND) 是另一个基本二元逻辑。

• 名称：与逻辑
• 算式表示方法：$A\cdot B$或$AB$，使用情况类似代数中乘号的省略问题
• 意义：只有当$A$与$B$都发生时，$X$才发生
• 等价开关电路：两开关串联（图中两保管员开关）
• 逻辑符号：

  

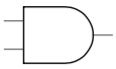
• 真值表：

$A$	$B$	$X$
0	0	0
0	1	0
1	0	0
1	1	1

同样地，通过真值表可以发现与逻辑类似乘法运算，且结果为 1 的概率有 25%。

四、异或逻辑

异或 (XOR) 是较为特殊的二元逻辑。

• 名称：异或
• 算式表示方法：$A\oplus B$（LaTeX 里这个符号不是很漂亮啊...）
• 意义：只有当$A$或$B$中有一个发生时，$X$才发生（注意和或逻辑的”只有“”只要“的区别！）
• 等价开关电路：双掷开关（用于两个开关同时控制一盏灯——任何一个开关变化都可以控制灯的亮灭）

  

  闭合状态，形成通路

  

  断开状态，不形成通路

• 逻辑符号：

  

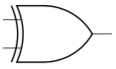
• 真值表：

$A$	$B$	$X$
0	0	0
0	1	1
1	0	1
1	1	0

通过真值表，可以发现，如果不考虑进位，异或运算才是真·二进制加法！实际上，异或又叫做“模二和”，加法器就是用异或实现的。也注意到，结果为 1 的概率是 50%。

五、同或逻辑

同或 (XNOR) 是另一种特殊的二元逻辑。

• 名称：同或
• 算式表示方法：$A\odot B$
• 意义：只有当$A$与$B$都发生或都不发生时，$X$才发生
• 等价开关电路：双掷开关
• 逻辑符号：

  

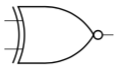
  以后会常常见到输入端或输出端的这个小圆圈——它表示额外的一步非运算

• 真值表：

$A$	$B$	$X$
0	0	1
0	1	0
1	0	0
1	1	1

观察真值表，发现异或和同或是相反运算（当自变量取值相同时，因变量值相反），解释了符号中小圆圈的意义。同或的使用相对不如异或频繁。

六、复合逻辑

除了以上五种逻辑，还有几种也成为了值得关注的逻辑。它们统称为复合逻辑。

复合逻辑使用较为广泛，但能很方便地用与、或、非表示，因此并没有自己的运算符号和特殊的逻辑符号。它们包括：与非 (NAND)$(AB)'$、或非 (NOR)$(A+B)'$，以及多元运算与或非$(A+BC)'$。与非和或非的逻辑符号都是在与符号和或符号的输出端上添一个小圆圈。

---

那么，以上逻辑的使用场景有什么呢？我们再次回到档案室的问题。当时提到一句话：

当“主任的钥匙插入”或者“‘档案保管员 A 的钥匙插入’而且‘档案保管员 B 的钥匙插入’”而且“防盗装置 未开启时，门锁打开

所有的重点词汇都已经着重标出。不难看到，它们分别对应了或、与、非的运算。那么，我们初步把它改写一下：

$$\begin{aligned} 门锁开启=(主任的钥匙插入+保管员A钥匙插入\cdot 保管员B钥匙插入)\cdot(防盗系统开启)' \end{aligned}$$

这其中比较难理解的一点是我们要先看防盗系统有没有开启再讨论钥匙的情况。当防盗系统开启时，该项取反后值为 0，无论前面一串是什么值，在与逻辑下结果都为 0，即门锁不开。

再换一种更直观的写法：

当
{
    主任的钥匙插入 or
    {
        保管员A的钥匙插入 and 保管员B的钥匙插入
    }
} and (not 防盗系统开启)
时
    门锁开启

甚至，更进一步，我们用字母代替每一事件，就像在第一章中做的那样，就能得到一个抽象的函数式$X=(A+B\cdot C)\cdot D'$。这个函数看似很抽象，实际上和上面一段话是完全等价的，就好像$y=7x$这个抽象的函数式可以用来表示“汽车每开 100 公里消耗 7 升油”一样。

就这样，我们已经通过直接分析文字描述的方法，写出了第一个逻辑函数式——别看这种方法显得笨拙，有时候，它得到的结果恰恰是最简洁的。而有了这个函数式，设计数字电路便会方便许多。